special EAEA
 |
|
 |
ARCHITECTURE AND MODERN INFORMATION TECHNOLOGIES
ÌÅÆÄÓÍÀÐÎÄÍÛÉ ÝËÅÊÒÐÎÍÍÛÉ ÍÀÓ×ÍÎ-ÎÁÐÀÇÎÂÀÒÅËÜÍÛÉ ÆÓÐÍÀË ÏÎ ÍÀÓ×ÍÎ-ÒÅÕÍÈ×ÅÑÊÈÌ È Ó×ÅÁÍÎ-ÌÅÒÎÄÈ×ÅÑÊÈÌ ÀÑÏÅÊÒÀÌ ÑÎÂÐÅÌÅÍÍÎÃÎ ÀÐÕÈÒÅÊÒÓÐÍÎÃÎ ÎÁÐÀÇÎÂÀÍÈß È ÏÐÎÅÊÒÈÐÎÂÀÍÈß Ñ ÈÑÏÎËÜÇÎÂÀÍÈÅÌ ÂÈÄÅÎ È ÊÎÌÏÜÞÒÅÐÍÛÕ ÒÅÕÍÎËÎÃÈÉ
TOPOLOGICAL METHOD OF CONSTRUCTION OF POINT SURFACES AS PHYSICAL MODELS
Dmitri Kozlov
NIITAG RAASN, Moscow, RUSSIA
Keywords: topology, manifold, knots, point surface, physical model
The shape of architectural objects in general can be treated as an envelope – a two dimensional surface embedded into three dimensional space. We directly perceive only the surface as a synthesis of sequential “photo snaps” – the two dimensional imprints on a retina – a concave screen inside of our eyes. In 15th century Italian architect and theorist L. B. Alberti claimed that the architecture consists in the outlines and the structure (lineamenta et structura in the original Latin text) [1]. The visible shape (outlines) exists only because a directly not perceived structure determines it. Like Alberti, the modern mathematical theories of form distinguish the shape as an exterior surface and the form itself as an internal structure [2]. This subtle difference becomes a very important subject in the relationship between a virtual and a physical model in the studies of architectural endoscopy.
The most general variety of geometry – topology – treats surfaces in three dimensional space as two dimensional manifolds – oriented and nonoriented. In the middle of 19th century it was proved that any oriented manifold is equal to a surface of a pretzel with a some number of holes in it or a sphere with the same number of handles [3]. The number of holes or handles is called “surface genus”, which equals to zero for a sphere, one for torus – the surface with one hole in it, two for a pretzel with two holes and so on. Each surface can be divided into a number of polygonal meshes or facets (F) with borders or edges (E) between them, which intersect in points or vertexes (V). These three elements of an any surface are interrelated and connected by a simple equation known as Eulerian index of a surface: V − E + F = 2 − 2n, there n is the number of the surface genus. So for each division of spherical surface – for all possible polyhedrons – Eulerian index is 2, and for any torus it is 0.
The topological approach to the problem of physical or virtual modelling of surfaces makes it possible to distinguish between a form and a shape as well as between a structure and an outline. Moreover, topology gives us new tools of describing, modelling and practical work with the objects, which till the recent times remained completely in the field of abstract mathematics.
Modelling of the architectural shape as well as any shapes, follows common logic of our perception of a spatial object. Practically it is more convenient to us to work with models on a plane like sketches, prospect drawings or computer graphic images on a display. In the same way it is more convenient to create the surfaces of three-dimensional objects in two-dimensional space as their developments, evolvements, patterns, etc. As a result, the practical possibilities of physical modelling of spatial surfaces are determined in general by the properties and structure of a material chosen for its plane development. This is the case of a practically perfect identity of a visible shape and the structure forming it.
Developable surfaces represents the elementary case of transition from a solid structure of flat sheet, such as a sheet of a paper, metal or plastic, to a fragment of a surface in three-dimensional space. It is possible also to divide a solid sheet into a number of facets (fragments of planes) and turning connections between them in order to create a flat folded development of a surface (Fig. 1). But this method allows creating only faceted approximations of real three dimensional curvilinear surfaces.
|
| |
| Fig. 1. Creation of a folded surface from its flat development |
It is possible also to turn from the solid planes to their linear approximations or edge models, such as fabrics, nets, lattices and grids. The edges can be flexible, elastic or rigid, and join together by means of friction or with hinges, like riveted joints, or any other turning connections. The structures of edge models of surfaces may be different, such as fabrics – the interweaved orthogonal threads of warp and weft, nets with knots like a fishing net, elastic lattices and weaves of flexible rods or twigs and kinematical grids of rigid rods with hinging.
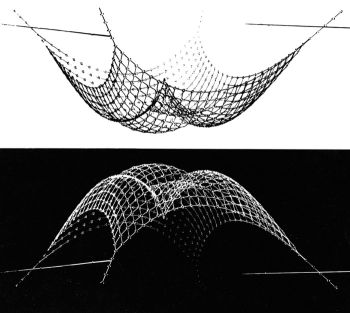
The principle of fabric structure has found its wide application in practical modelling of complex curvilinear surfaces. Russian mathematician P. L. Chebyshev in 1878 has stated mathematical principles for flat developments of curvilinear surfaces from fabric with square meshes [4]. Another important direction in form-finding with edge models of plane is inverting flexible hanging nets formed from a planar state by force of gravitation in order to receive the support surface of a grid shell free of moments (Fig. 2).
 |
|
| Fig. 2. Inverting of flexible hanging nets as a method of form finding |
This method was yielded by analogy with a suspended chain forming a catenary which been inverted becomes the thrust line of an arch free of moments. Famous Spanish architect A. Gaudi was the first who in the end of 19th century started experiments with suspended models made of strings as a form-finding method in architecture. Gaudi sought the structural forms which were free of moments and shearing forces. He was interested also in their formal aspect – the fact that one could visually follow the flow of forces in the structure. Gaudi approximated the catenary with parabolic arches in his early structures, but lately he made several spatial suspended string models for his churches. When the models were inverted, the polygons formed by the strings yielded the directions of the supports. In the end of 1940th German architect and engineer F. Otto started his own experiments with suspended models made of fabric saturated with liquid plaster of Paris. The original task of this work was to discover forms suitable for vaulted roofs, but lately it became the basis of the grid shells building theory, resulted in several architectural masterpieces by F. Otto and his team [5].
However facet and linear models do not exhaust all possibilities of plane approximations. Eulerian formula for 2 manifolds demonstrates that there are three topological elements of surfaces: two dimensional facets, one-dimensional edges and zero dimensional vertexes. Because of this, it must be the third model of plane – namely vertex or point surfaces. But the question is: what are the physical models of such plane point surfaces and how to transform them from planar into spatial position?
First of all, the point set must be topologically connected in order to work like a continual model of a plane point surface. Secondly, the connecting structure must provide the points with possibility of free movement and let them stay relatively independent of each other. At first glance these two demands contradict each other, but actually only topologically connected structure can provide the point set with some sort of functional discontinuity and freedom.
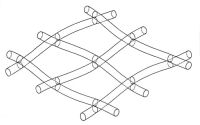
For example, a good approximation of a piece of point surface is a fabric of woven elastic and flexible rods like surface of a basket of fresh twigs (Fig. 3). But this structure functions like a linear model of a plane because its transformation into a fragment of spatial surface is a result of deformation of rods or twigs and not of point’s movement. Consequently, a fragmentary model of a point surface do not guarantee its behaviour as a demanded plain vertex model, because the most important part – namely the structure – is missing.
 |
|
| Fig.3. A model of point surface made of woven elastic and flexible rods |
There is a natural phenomenon connected with flexible-elastic tissues which got a name of resilience in bio-mechanics [6]. It is defined as a certain quality of elastic energy, accumulated in a material of a structure without causing any damage to it. But this very deformation growing progressively contributes to the better accumulation of elastic energy, lessening of the weight of the structure and increasing of its durability. Natural string-like flexible-elastic long objects, e.g. polymeric molecules like DNA, can wind, cross themselves and often they occur in circular closed form [7]. In certain instances this trend leads to forms of rings and knots either single or linked. Knots and links are widespread and natural way of structural organization for string-like flexible-elastic long objects.
Experimental research of different plain vertex models performed by the author, confirmed that the most natural forms of organizing independent point contacts into topologically connected structures are cyclic or periodical knots and links [8]. An elastic and flexible rod forms the elementary structure then its ends are joined together (Fig. 4(a)). As a result the rod becomes a ring (a trivial knot), and its structural stability depends on the ratio between the diameter of the ring and diameter of cross-section of the rod. Then the diameter of the ring is too large to resist the inner torsion forces in the bent rod, the ring turns into double nested loops or topological solitons (Fig. 4(b)).
If the process of loops emerging is combined with joining together the free ends of the rod, the connected rod possibly will be knotted – it will take the form of the simplest knot known as “trefoil” (Fig. 4(c)). The process of “self-knotting” is very typical for long flexible-elastic strings, such as steel wire or fishing-line.
|
| |||||||
| Fig. 4(a,b,c). a. A ring (trivial knot) of flexible rod; b. A double nested loop; c. A simplest knot – trefoil |
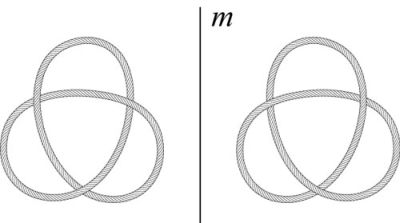
The trefoil knot is not only the simplest knot but also “torus knot”, because it can be placed without any self-crossings on the surface of a torus. A torus is a topological 2 manifolds and its genus of surface is equals to 1. Analogously to trefoil, there are knots that can be placed on the surfaces of another 2 manifolds with the genus more then 1 – the surfaces of pretzels with two or more holes in them. A trefoil knot may have two mirror types – a “left” and a “right” (Fig. 5).
|
| |
| Fig. 5. Two mirror types of the trefoil |
Each of them can be tied on the torus surface without self-crossings (Fig. 6(a,b)), but been tied together on the same torus, they inevitably cross each other as two coming from the opposite direction spatial spirals (Fig.6(c)).
|
| |
| Fig. 6(a,b,c). a, b. A left and right trefoil can be tied on the torus surface without self-crossings; c. Both trefoils tied together on the same torus inevitably cross each other |
As a result we get an elementary knotted fabric on the torus surface. If both knots made of flexible-elastic material and their crossings are really contacting, the structure will represent a model of torus point surface. It is important to emphasize here: the contacting points define the model of the surface – namely the exterior shape and two mirror knots form its interior structure. In the same way we can build a point surface of an arbitrary pretzel with two mirror pretzel knots of appropriate type. So this is a universal method of modelling the 2 manifolds as point surfaces.
The quantity of elastic energy in a knotted rod depends of knot’s topological complexity and is known among other topological invariants of knots [9]. But this inner elastic energy plays a key part for the knots used as structures of plain vertex models. Thanks to this energy, the central lines of knotted rods tend to coincide with flatness, so all their crossings tend to be really contacted and form a model of flat point surface.
The considered above two mirror trefoils on the torus surface also must tend to collapse and if the torus itself disappeared, the contacting points of the two knots would place themselves in a flat ring-shaped area. And vice versa: a flat model of point surface, given by a cyclic knot or a link of several cyclic knots, may be transformed into a spatial state and fixed in it in order to keep the received shape. The main condition of the possibility to transform a cyclic knot from flat state to a spatial one is a sufficient number of its contacting crossings, that is a detailed enough model of point surface.
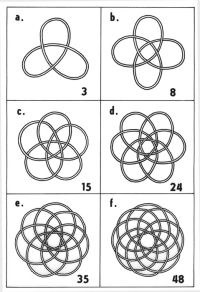
The number of crossing points depends of the number of loops and consequently – of the total structural energy of knotted rods. Increasing of structural energy proportionally to the number of loops and the quantity of contacting crossings leads to a new property of knots. From the simplest knots like a trefoil they grow into complicated structures, which scarcely can be named “knots” in the common sense of the word, as something assigned for tying or binding. The Fig. 7(a f) shows the sequence of cyclic knots started from the trefoil, that has 3 loops and 3 crossings.
|
| |
| Fig. 7(a-f). The sequence of cyclic knots derived from the trefoil |
The quantity of the loops grows according to the row of natural numbers (3, 4, 5, 6, 7, 8 …), but the corresponding quantity of the crossings grows as an arithmetic progression of second-order (3, 8, 15, 24, 35, 48 …). These cyclic knotted structures designed specially for modelling of the point surfaces – both flat and spatial – the author named “NODUS” structures (the word “nodus” means “a knot” in Latin) [10].
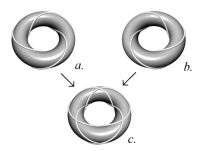
A NODUS structure during its transformation process changes the lengths of the edges of all its facets and angles between them. Thanks to that ability, the structure changes its geometry as a whole and creates vertex or point models of the shapes with an arbitrary Gaussian curvature: parabolic, elliptic or hyperbolic. These three types of surfaces completely exhaust all possible internal geometries of 2 manifolds [11]. But as opposed to solid models of surfaces, that can not change their Gaussian curvatures without breaks and folds, the point surfaces of NODUS structures permit the transition from the positive Gaussian curvature (elliptic) to the negative one (hyperbolic) through the mediation of neutral (parabolic) curvature. The same NODUS structure can take the shapes of an elliptic (Fig. 8(a)) and a hyperbolic (Fig. 8(b)) curvature. The torus shape (Fig. 8(c)) is a combination of these two types of curvatures together with two intermediate areas of parabolic curvature. It is possible also to create many other shapes, including asymmetrical and combined ones.
 |
 |
 |
|
a) |
b) |
c) | |
| Fig. 8(a-c). a. A NODUS structure as a model of surface with elliptic curvature; b. The same structure, but turned inside out yields a model of surface with hyperbolic curvature; c. A torus model as a combination of two fragments of surfaces with elliptic and hyperbolic curvatures | |||
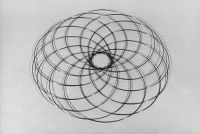
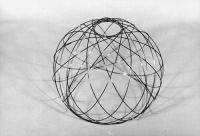
Apart from the transformation of NODUS structures that change the sign of its curvature and which can be named “qualitative transformation”, there is another kind of transformation – the “quantitative” one. This transformation happens as a gradual changing of numerical value of Gaussian curvature of point surface from its minimum to a maximum value without an alteration of the curvature sign. The minimum value of Gaussian curvature may be equals to zero, and in this case the point surface of a NODUS structure approximates a piece of flatness. Its transformational process represents a continual sequence of changing shapes, for example from spherical segment through hemisphere to sphere (Fig. 9(a e)).
 |
 |
 | |||
a) |
b) |
c) |
 |
 | ||
d) |
e) |
Fig. 9(a-e). Transformation of a NODUS structure as a continual sequence of changing shapes from flatness through spherical segment and hemisphere to sphere
This process of transformation is reversible. Changing its shape, the NODUS structure accumulates elastic energy and strengthens itself. Any spatial position may be strictly fixed by limitation of the structure’s kinematics ability. In this case a transformable NODUS structure will be turned into a static one.
The topological essence of the NODUS structures as changeable point surfaces allows extrapolating the structural properties of their models to the large-sized structures (Fig. 10(a c)) [12]. Such awareness may arise from the study of the experience of Buckminster Fuller, whose geometric structures are equally workable from the molecular sizes to the gigantic domes.
 |
 |
 | |||
a) |
b) |
c) |
Fig. 10(a-c). A test model of large sized NODUS structure in different stages of transformation
The polymorphous kinematical possibilities of NODUS structures give an architect or a designer a suitable tool not only for finding the demanded form in space, but also for “tuning” it in the environment. It is possible to envision in advance the script of development of planar point model into a model of a surface in three-dimensional space by different dispositions of modular form-generating structures on a plane, by choice of their connections and by space stratifications of contact point groups. Being essentially independent of a computer, the given method of form-finding and modelling of surfaces can be presented also in a virtual aspect by mean of creation of special computer programs or adapting already existing 3D editors. The algorithmic method of the analysis of the arranged point sets merged by connected intermediary structure, allows speaking about a uniform method for both virtual and physical modelling of surfaces in three-dimensional space. The physical nature of form-generating polymorphous NODUS structures allows considering them also as a basis of real-size kinematical architectural structures.
References
1. Alberti L. B. Ten Books on Architecture. // All-Union Academy of Architecture, Moscow. Volume 1 – 1935; Volume 2. – 1937. (in Russian)
2. Lord E. A., Wilson C. B. // The Mathematical Description of Shape and Form. John Wiley & Sons, New York, 1984.
3. Thurston W.P. The mathematics of three-dimensional manifolds. / Weeks J.R. // Scientific American, July 1984, pp 94 - 106.
4. Chebyshev P. L. Sur la Coupe des Vêtements // Complete works by P. L. Chebyshev. Volume V. Academy of Sciences of USSR, Moscow – Leningrad, 1951. p. 165 – 170 (in Russian).
5. Otto F. and others. Grid Shells. // Institute for Lightweight Structures (IL-10), University of Stuttgart, Stuttgart 1974.
6. Lebedev Yu. S. and others. Architectural Bionics. // Stroyizdat, Moscow. 1990. (in Russian)
7. Liu L. F. Knotted Single-stranded DNA Rings / Depew R. E., Wang J.C. // Journal of Molecular Biology, 1976.-Vol. 106. p. 439 – 452.
8. Kozlov D. Yu. Regular knots and links as a structural principle of kinetic architectural structures // Scientific works of The Laboratory of Architectural Bionics. Published by TSNIIEP Zhilischa, Moscow, 1989. (in Russian)
9. Stewart I. Finding the Energy to Solve a Knotty Problem // New Scientist. March 1993. 18 p.
10. Kozlov D. Yu. Polymorphous resilient-flexible shaping structures “NODUS” for space and other extreme environments // Final Conference Proceedings Report of The First International Design for Extreme Environments Assembly (IDEEA ONE), University of Houston. Houston, 1991. p. 259 – 260.
11. Hilbert D., Cohn-Vossen S. Geometry and the Imagination. // Chelsea, New York. 1999.
12. Kozlov D. Yu. Dome structures for flexible material // Roofs. Part 1. Human settlements and socio-cultural environment. Paris, UNESCO, 1991. p. 127 – 131.